
Avr 12, 2024 | Actualité, DSHE, Prix et distinctions, Recherche
Notre collègue Philippe Brunet, physicien directeur de recherche au CNRS, a été élu “Outstanding Referee of the Year” par l’American Physical Society. L’APS publie chaque année une liste de 150 referee exceptionnels par le nombre, la qualité et...
Mar 28, 2024 | Actualité, MSC, Recherche, Théorie
Dans un travail récent, des physiciennes et un physicien montrent comment l’hétérogénéité spatiale et relationnelle est un ingrédient indispensable au maintien à long terme d’une diversité écologique importante dans les vastes écosystèmes naturels. Comprendre les...
Mar 28, 2024 | Actualité, MSC, Recherche
L’origine de l’homme est une question importante, une des plus passionnante scientifiquement. Les travaux sur cette question sont essentiellement des travaux de paléontologie, d’une part, et des travaux de paléogénomique d’autre part. Les premiers permettent...

Mar 12, 2024 | Actualité, DSHE, MSC, Prix et distinctions, Recherche
Les recherches de F. Novkovski et E. Falcon sur le magnétisme donnent lieu à des images étonnantes, primées lors de la dernière édition du concours “La Preuve par l’Image” organisé par le CNRS Nul tour de magie derrière les étranges oscillations de...

Mar 8, 2024 | Actualité, MSC
Le laboratoire MSC a la grande tristesse d’annoncer le décès de notre collègue et ami, Julien Moukhtar. Julien Moukhtar en compagnie de Philippe Brunet (gauche) et Laurent Royon (droite), au laboratoire MSC Il est parti le 5 mars 2024 sans souffrir, en présence...

Fév 26, 2024 | Actualité, MSC, Prix et distinctions
Notre collègue Florence Gazeau, Directrice adjointe du laboratoire et responsable de l’équipe interdisciplinaire « MSC-med » implantée à l’école de Médecine de l’Université de Paris-Cité, s’est vu attribuer la Médaille d’Argent 2024 du CNRS pour l’ensemble de ses...
Jan 15, 2024 | A venir., Actualité, Doctorants / Post-doctorants, MSC
Richard Amedzrovi Agbesi’s PhD thesis defense will take place on Friday, January 19th at 2:00 PM in the Pierre Gilles de Gennes Amphitheater.This thesis, supervised by Nicolas Chevalier and Vincent Fleury, focuses on the Fundamentals of intestinal peristalsis:...
Nov 26, 2023 | Actualité, MSC
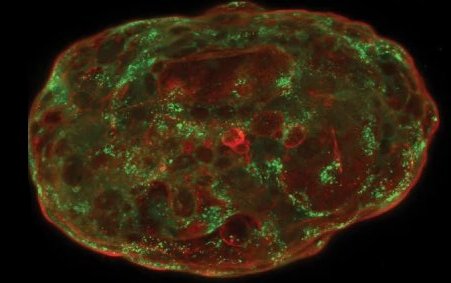
Formés à partir de cellules souches embryonnaires humaines, des simili d’embryons peuvent maintenant être cultivés in vitro jusqu’à mimer 14 jours de développement embryonnaire naturel, ouvrant la voie à des applications aussi bien fondamentales qu’appliquées. Quelles...

Nov 22, 2023 | Actualité, MSC
En s’écoulant sur des roches solubles, l’eau peut créer dans la nature des motifs remarquables, qui présentent souvent des pointes acérées. Les coups de gouge, dépressions concaves entourées de crêtes, en sont un exemple commun. En combinant mesures de terrain, modèle...











